x+y y +x (and associativity)
x+y y +x (and associativity)
Applying the axiom to expressions (making a multiway graph)
Applying the axiom to expressions (making a multiway graph)
In[]:=
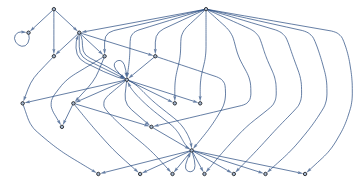
NestGraph[Flatten[{Values[substitutionLemmas[#,x_⊕y_y_⊕x_]]}]&,(a⊕b)⊕(c⊕d),5,VertexLabelsAutomatic,GraphLayout"LayeredDigraphEmbedding",AspectRatio1]
Out[]=
In[]:=
Graph[ResourceFunction["MultiwayFunctionSystem"][Values[substitutionLemmas[#,x_⊕y_y_⊕x_]]&,(a⊕b)⊕(c⊕d),5,"StatesGraph"],GraphLayout"LayeredDigraphEmbedding",AspectRatio1]
Out[]=
In[]:=
With[{g=NestGraph[Flatten[{Values[substitutionLemmas[#,x_⊕y_y_⊕x_]]}]&,(a⊕b)⊕(c⊕d),5,VertexLabelsAutomatic]},HighlightGraph[g,Style[PathGraph[FindShortestPath[g,(a⊕b)⊕(c⊕d),(d⊕c)⊕(b⊕a)],DirectedEdgesTrue],Red,Thick],GraphLayout"LayeredDigraphEmbedding",AspectRatio1]]
Out[]=
Note that there are multiple proofs of the same result....
In[]:=
With[{g=NestGraph[Flatten[{Values[substitutionLemmas[#,x_⊕y_y_⊕x_]]}]&,(a⊕b)⊕(c⊕d),5,VertexLabelsAutomatic]},FindShortestPath[g,(a⊕b)⊕(c⊕d),(d⊕c)⊕(b⊕a)]]//Column
Out[]=
(a⊕b)⊕(c⊕d) |
(a⊕b)⊕(d⊕c) |
(b⊕a)⊕(d⊕c) |
(d⊕c)⊕(b⊕a) |
In[]:=
Labeled[c,Style[x,Small]]⊕Labeled[d,Style[y,Small]]
Out[]=
x |
y |
[[[[ This is self-applied, so doesn’t work ]]]]
In[]:=
TwoWayMultiReplaceGraphList[{x_⊕y_y_⊕x_},3,"CoSubstitutionLemmas"->False,"Deduplicate"->True,"Canonicalize"->False,"RuleSelectionFunction"->(Tuples[{Range[1],Range@Length@#}]&)]
Out[]=
,
,
,
In[]:=
TwoWayMultiReplaceGraphList[{x_⊕y_y_⊕x_,(a⊕b)⊕(c⊕d)<->True},5,"CoSubstitutionLemmas"->False,"Deduplicate"->True,"Canonicalize"->False,"RuleSelectionFunction"->(Append[DeleteCases[Tuples[{Range[1],Range@Length@#}],{1,1}],{2,2}]&)]
Out[]=
,
,
,
,
,
In[]:=
VertexList
Out[]=
{(a⊕b)⊕(c⊕d)True,TrueTrue,(a⊕b)⊕(c⊕d)(a⊕b)⊕(c⊕d),(b⊕a)⊕(c⊕d)(a⊕b)⊕(c⊕d),x_⊕y_y_⊕x_,(a⊕b)⊕(d⊕c)(a⊕b)⊕(c⊕d),(c⊕d)⊕(a⊕b)(a⊕b)⊕(c⊕d),True(a⊕b)⊕(c⊕d),(c⊕d)⊕(a⊕b)(b⊕a)⊕(c⊕d),(c⊕d)⊕(a⊕b)(a⊕b)⊕(d⊕c),(c⊕d)⊕(a⊕b)True,(d⊕c)⊕(a⊕b)(a⊕b)⊕(c⊕d),(c⊕d)⊕(b⊕a)(a⊕b)⊕(c⊕d),(c⊕d)⊕(a⊕b)(c⊕d)⊕(a⊕b),(b⊕a)⊕(c⊕d)(b⊕a)⊕(c⊕d),(b⊕a)⊕(c⊕d)(a⊕b)⊕(d⊕c),(a⊕b)⊕(c⊕d)(a⊕b)⊕(d⊕c),True(a⊕b)⊕(d⊕c),(d⊕c)⊕(a⊕b)(a⊕b)⊕(d⊕c),(c⊕d)⊕(b⊕a)(a⊕b)⊕(d⊕c),(c⊕d)⊕(a⊕b)(b⊕a)⊕(d⊕c),(c⊕d)⊕(a⊕b)(d⊕c)⊕(a⊕b),(a⊕b)⊕(c⊕d)(c⊕d)⊕(a⊕b),(a⊕b)⊕(d⊕c)(a⊕b)⊕(d⊕c),(a⊕b)⊕(c⊕d)(d⊕c)⊕(a⊕b),(a⊕b)⊕(c⊕d)(c⊕d)⊕(b⊕a),(a⊕b)⊕(c⊕d)(b⊕a)⊕(c⊕d),(a⊕b)⊕(c⊕d)(b⊕a)⊕(d⊕c)}
Including associativity
Including associativity
In[]:=
Graph[ResourceFunction["MultiwayFunctionSystem"][Values[substitutionLemmas[#,x_⊕(y_⊕z_)(x_⊕y_)⊕z_]]&,(a⊕b)⊕(c⊕d),5,"StatesGraph"],GraphLayout"LayeredDigraphEmbedding",AspectRatio1]
Out[]=
Applying to Expressions, but Generating Variables
Applying to Expressions, but Generating Variables
[[ Any time you’re not just rearranging structure, you potentially have to generate variables ]]
[ Similar issue to generating atoms of space ]
[ Similar issue to generating atoms of space ]
This is generating the same literal x_ every time
(it is not a constant because it still matches ... but all instances of x_ have to match the same thing)
(it is not a constant because it still matches ... but all instances of x_ have to match the same thing)
This uses a constant a :
[[ This has both a and a_ ]]
[A two-way rule will have the variables-need-to-be-generated issue in a way that one-way rules will not]
[A two-way rule will have the variables-need-to-be-generated issue in a way that one-way rules will not]
Boolean algebra example
Boolean algebra example
Trying to establish:
Applying the Axioms to Statements
Applying the Axioms to Statements
This is a code ≠ data situation: the axiom are the code, the statements are the data ... but now the code and data are basically in the same format....
Typical statement:
[ A not very useful statement ]
Self-applying to the axiom
Self-applying to the axiom
Canonicalize under pattern/variable renaming:
Accumulative
Accumulative
[[[ Not very natural without TEGs ... ]]] [ Effectively what one would do is collect every statement into a single state on which to apply a rule that picks up pairs of statements ]
Purely Self Applying [aka the “Gas of Statements”]
Purely Self Applying [aka the “Gas of Statements”]
self-applying == “bootstrapping”
self-applying == “bootstrapping”
(AKA “pool of statements”, “vat of statements”, ...)
These are “actually generated” statements (living in metamathematical space) .... as opposed to statements which are syntactic but which don’t necessarily get generated
Start with initial statements, then let them “interact”
Start with initial statements, then let them “interact”
The token-event graph is “naturally accumulative”
The token-event graph is “naturally accumulative”
[[ Not such a useful deduplication ]]
In this case, the universe ends........
Variable generating case:
Variable generating case:
In each case, we can get the pure MW states graph like this:
In each case, we can get the pure MW states graph like this:
[[ Note that a ↔ a is somewhere in the middle ]]
This is too complicated:
E.g. Boolean algebra
E.g. Boolean algebra
The following is presumably wrong:
Possibly pure substitution is enough because there is a single variable on one side
Ordinary Boolean algebra
Ordinary Boolean algebra
Will pure substitution give all true statements of Boolean algebra?
Combinator / Machine-Code Level
Combinator / Machine-Code Level
[[ This is below standard axiomatic mathematics ]]
Start from all possible combinator expressions
with a certain “law of application”
with a certain “law of application”
Certain collection of combinator expressions can be “identified as having a meaning/purpose”
(cf recruitment of molecules for life)
(cf recruitment of molecules for life)
“Definitional entailment” (AKA “interpretation step”)
“Definitional entailment” (AKA “interpretation step”)
As soon as one finds a “cluster” of combinator expressions that match the LHS ... we can now identify the lumps of combinators with the specified names
How does one piggyback on the raw combinators to make a describable computation?
[cf “How do you make a switch out of magnetic bubbles” ... ]
In general, there are many ways to make e.g. Plus at the combinator level
In general, there are many ways to make e.g. Plus at the combinator level
The fact that there many ways to do this (and they’re decently dense in syntactic space) makes this “a robust concept”
This is analogous to emergent language design: i.e. if there’s a common cluster of combinators, give it a name
This is analogous to emergent language design: i.e. if there’s a common cluster of combinators, give it a name
Probably: syntactic density depends on reference frame
Probably: syntactic density depends on reference frame