Accumulate on Inactive lists
[for S7 combinator growth]
Accumulate on Inactive lists
[for S7 combinator growth]
[for S7 combinator growth]
Jose, Dec 3, 2020
Original expression
Original expression
block[n_]=Inactive[Join][38{0,0,0,12,-17}+{0,1,0,-135,189},Inactive[Table][0,{i,n}],38{0,1,0,0,1,-1,0,0,0,4}+{12,-13,0,6,-7,1,0,1,0,-27},Inactive[Table][0,{i,n+2}],228{0,1,0,0,1,-1}+2{6,-20,0,3,-17,14}]
n
2
n
2
n
2
Join[{0,1,0,-135+57,189-323},Table[0,{i,n}],{12,-13+19,0,6,-7+19,1-19,0,1,0,-27+19},Table[0,{i,2+n}],{12,-40+57,0,6,-34+57,28-57}]
3+n
2
1+n
2
1+n
2
1+n
2
1+n
2
3+n
2
2+n
2
2+n
2
2+n
2
nmax=200;
blocks0=Flatten@Activate[Table[block[n],{n,nmax}]];
blocks1=Accumulate[blocks0];
blocks2=Accumulate[blocks1];
len=Length[blocks0]
44800
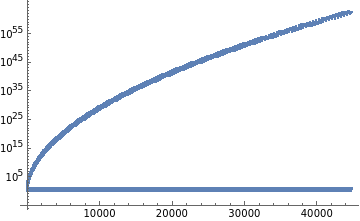
ListLogPlot[blocks0]
ListLogPlot[blocks1]
ListLogPlot[blocks2]
Manipulation of inactive lists
Manipulation of inactive lists
Idea
Idea
We will work on lists, Inactive[Table][body, {i, n}] and Inactive[Join][...].
We are interested in the operations Length, Total and Accumulate.
Length
Length
length[list_List]:=Length[list];length[Inactive[Table][body_,{k_,n_}]]:=n;length[Inactive[Join][lists___]]:=Total[length/@{lists}];
Total
Total
total[list_List]:=Total[total/@list];total[Inactive[Table][body_,it_]]:=Sum[body,it];total[Inactive[Join][lists___]]:=Total[total/@{lists}];total[x_]:=x;
mean[expr_]:=total[expr]/length[expr]
Accumulate
Accumulate
accumulate[list_]:=accumulate[0,list];accumulate[n_,Inactive[Join][lists__]]:=accumulateFold[n,lists]
accumulateFold[seed_]:=Inactive[Join][];accumulateFold[seed_,list_List,rest___]:=With[{a=Simplify[seed+Accumulate[list]]},Join[Inactive[Join][a],accumulateFold[Last[a],rest]]];(*accumulateFold[seed_,Inactive[Table][0,{k_,n_}],rest___]:=Join[Inactive[Join][Inactive[Table][seed,{k,n}]],accumulateFold[seed,rest]];*)accumulateFold[seed_,Inactive[Table][body_,{k_,n_}],rest___]:=Join[Inactive[Join][Inactive[Table][Simplify[seed+Sum[body,{K,k}]],{k,n}]],accumulateFold[seed+Sum[body,{K,n}],rest]]
First integration
First integration
accumulate[block[n]]
Join[{0,1,1,-134+57,55-95},Table[55-95,{i,n}],{67-95,54-19,54-19,60-19,53-57,54-19,54-19,55-19,55-19,28},Table[28,{i,2+n}],{40,57,57,6+57,-28+57,57}]
3+n
2
1+n
2
1+n
2
1+n
2
3+n
2
3+n
2
3+n
2
1+n
2
3+n
2
3+n
2
3+n
2
3+n
2
2+n
2
2+n
2
2+n
2
3+n
2
2+n
2
Add all last elements:
sum1[n_]=Sum[57,{i,1,n}]
2+i
2
456(-1+)
n
2
Shifted blocks:
acblock[n_]=accumulate[sum1[n-1],block[n]]
Join[{228(-2+),-455+57,-455+57,-590+171,-401+19},Table[-401+19,{i,n}],{-389+19,-402+19,-402+19,4(-99+19),-403+57,-402+19,-402+19,-401+19,-401+19,4(-107+57)},Table[4(-107+57),{i,2+n}],{4(-104+57),456(-1+),456(-1+),-450+57,4(-121+171),456(-1+)}]
n
2
2+n
2
2+n
2
2+n
2
1+n
2
1+n
2
1+n
2
2+n
2
2+n
2
n
2
1+n
2
2+n
2
2+n
2
2+n
2
2+n
2
n
2
n
2
n
2
n
2
n
2
3+n
2
n
2
n
2
Check:
Activate[Join@@Table[acblock[n],{n,1,nmax}]]===blocks1
True
Second integration
Second integration
accumulate[acblock[n]]
Join[{228(-2+),-911+57,-1366+171,-1956+171,-2357+703},Table[-2357+703+(-401+19)i,{i,n}],{-2746+361+(-401+19)n,-3148+95+(-401+19)n,-3550+399+(-401+19)n,-3946+209+(-401+19)n,-4349+893+(-401+19)n,-4751+931+(-401+19)n,-5153+969+(-401+19)n,-5554+1007-401n+19n,-5955+1045+(-401+19)n,-6383+1159+(-401+19)n},Table[-6383+1159+4(-107+57)i+(-401+19)n,{i,2+n}],{-7655+1501+(-829+133)n,-8111+1729+(-829+133)n,-8567+1957+(-829+133)n,-9017+2185+(-829+133)n,-9501+2527+(-829+133)n,-9957+2755+(-829+133)n}]
n
2
3+n
2
2+n
2
3+n
2
1+n
2
1+n
2
1+n
2
2+n
2
1+n
2
4+n
2
1+n
2
2+n
2
1+n
2
3+n
2
1+n
2
1+n
2
1+n
2
1+n
2
1+n
2
1+n
2
1+n
2
1+n
2
1+n
2
1+n
2
1+n
2
1+n
2
1+n
2
1+n
2
n
2
1+n
2
1+n
2
1+n
2
1+n
2
1+n
2
1+n
2
1+n
2
1+n
2
1+n
2
1+n
2
1+n
2
1+n
2
1+n
2
Add all last elements:
sum2[n_]=Sum[-9957+2755+(-829+133)i,{i,1,n}]
1+i
2
1+i
2
1
2
4+n
2
3+n
2
2
n
Shifted blocks:
acacblock[n_]=accumulate[sum2[n-1],acblock[n]]
Join-987+2603+-+133n-,(4(-721+2717)+(-19085+133)n-829),(-3794+2831+(-19085+133)n-829),(-4974+3173+(-19085+133)n-829),(-5776+399+(-19085+133)n-829),Table(-5776+399+(-802+19)i+(-19085+133)n-829),{i,n},(-6554+3211+(-19887+19)n-829),(-7358+3249+(-19887+19)n-829),(-8162+3287+(-19887+19)n-829),(-8954+3325+(-19887+19)n-829),(-9760+1691-19887n+19n-829),-5282+855+-+19n-,28(-203+247)+-+19n-,-6085+437+-+19n-,-6486+1767+-+19n-,-6914+57+-+19n-,Table-6914+57+4(-107+57)i+-+19n-,{i,2+n},-8186+1995+-+133n-,-8642+2109+-+133n-,-9098+2223+-+133n-,-9548+2337-+133n-,(20064(-1+)+(-20743+133)n-829),(20976(-1+)+(-20743+133)n-829)
1+n
2
19085
2
1+n
2
829
2
n
2
1
2
n
2
2+n
2
2
n
1
2
2+n
2
2+n
2
2
n
1
2
2+n
2
2+n
2
2
n
1
2
5+n
2
2+n
2
2
n
1
2
5+n
2
2+n
2
2+n
2
2
n
1
2
2+n
2
5+n
2
2
n
1
2
2+n
2
5+n
2
2
n
1
2
2+n
2
5+n
2
2
n
1
2
2+n
2
5+n
2
2
n
1
2
3+n
2
5+n
2
2
n
3+n
2
19887
2
4+n
2
829
2
n
2
n
2
19887
2
4+n
2
829
2
n
2
4+n
2
19887
2
4+n
2
829
2
n
2
2+n
2
19887
2
4+n
2
829
2
n
2
7+n
2
19887
2
4+n
2
829
2
n
2
7+n
2
n
2
19887
2
4+n
2
829
2
n
2
2+n
2
20743
2
2+n
2
829
2
n
2
2+n
2
20743
2
2+n
2
829
2
n
2
2+n
2
20743
2
2+n
2
829
2
n
2
2+n
2
20743n
2
2+n
2
829
2
n
2
1
2
n
2
3+n
2
2
n
1
2
n
2
3+n
2
2
n
Check:
All blocks behave in similar ways...
Main result
Main result
Given that the result is oscillatory, there are several options we can follow
Asymptotics
Asymptotics
Let us take the last element of the twice-accumulated block n (it would probably be better to compute the average of the block):
Those correspond to positions
Therefore what we want is
The agreement is quite good:
There is a residual oscillatory term in all cases. The mean seems more centered:
Finally:
Compare to Stephen’s result, which does not seem correct: